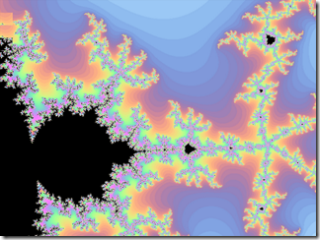
My friend George Foot suggested this improved version of the Mandelbrot shader I posted yesterday:
float4 PixelShader(float2 texCoord : TEXCOORD0) : COLOR0
{
float2 c = (texCoord - 0.5) * Zoom * float2(1, Aspect) - Pan;
float2 v = 0;
float m = 0;
const float r = 5;
for (int n = 0; n < Iterations; n++)
{
v = float2(v.x * v.x - v.y * v.y, v.x * v.y * 2) + c;
if (dot(v, v) < (r*r - 1))
m++;
v = clamp(v, -r, r);
}
if (m == Iterations)
return 0;
else
return float4(sin(m/4), sin(m/5), sin(m/7), 1) / 4 + 0.75;
}
This renders fractals in glorious technicolor:
A similar technique can also be used to render Julia sets, which are closely related to the Mandelbrot. To do this, the beginning of the pixel shader changes to:
float4 PixelShader(float2 texCoord : TEXCOORD0, float4 color : COLOR0) : COLOR0
{
float2 c = color;
float2 v = (texCoord - 0.5) * Zoom * float2(1, Aspect) - Pan;
float m = 0;
// the rest is identical to the above Mandelbrot shader
Julia sets are defined by a seed value, so we need a variable to store this in the C# code:
Vector2 julia = new Vector2(0.5f);
In the Update method, add a line using the right stick to control the seed position:
julia += new Vector2(pad.ThumbSticks.Right.X, -pad.ThumbSticks.Right.Y) * 0.005f;
And in the Draw method, change the SpriteBatch call to pass the seed into the pixel shader, via the sprite color parameter:
spriteBatch.Draw(dummyTexture, Vector2.Zero, new Color(new Vector3(julia, 0)));
Julia sets are if anything even more fascinating than the Mandelbrot. Different seed values can produce an incredible variety of patterns: